Introduction...
I hope it would be helpful to everyone.
This blog deals with various sutras mentioned by Sri Bharati Krshna Thirtha swamiji and taught by Sri Avadhanulu garu to me(Kaushik).
Sutras
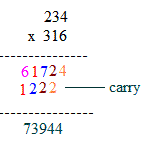
We now take examples of 1 / a9, where a = 1, 2, -----, 9. In the conversion of such vulgar fractions into recurring decimals, Ekadhikena Purvena process can be effectively used both in division and multiplication.
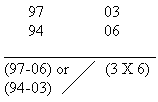 =91/18=9118
=91/18=9118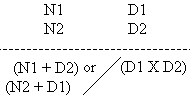


10/(-9)=91 how?
10/(-9) should be read as 'one zero, nine bar'. Here 'one' and 'zero' are in normal form. 'nine' is in complement form. so, when we bring a carry from normal form to complment form, '10' becomes '9' and '9-bar' becomes '1'( 10's complement of 9). Hence 10/(-9)-91.
Another example would be 94/(-3)=93/7=937.
Find the following products by Nikhilam formula.
1) 7 X 4 2) 93 X 85 3) 875 X 994 4) 1234 X 1002
5) 1003 X 997 6) 11112 X 9998 7) 1234 X 1002 8) 118 X 105

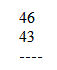
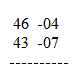
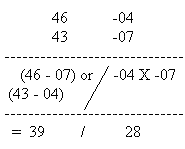

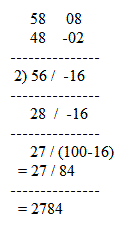
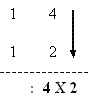
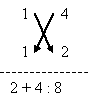

This Sutra means 'by addition and by subtraction'. It can be applied in solving a special type of simultaneous equations where the x - coefficients and the y - coefficients are found interchanged.
This sutra means whatever the extent of its deficiency, lessen it still further to that very extent; and also set up the square of that deficiency. This sutra is very handy in calculating squares of numbers near(lesser) to powers of 10
For instance in computing the square of 98 we go through the following steps:
1. The nearest power of 10 to 98 is 100.
2. Therefore, let us take 100 as our base.
3. Since 98 is 2 less than 100, we call 2 as the deficiency.
4. Decrease the given number further by an amount equal to the deficiency.
i.e., perform ( 98 -2 ) = 96. This is the left side of our answer!!.
5. On the right hand side put the square of the deficiency, that is square of 2 = 04.
6. Append the results from step 4 and 5 to get the result. Hence the answer is 9604.
Note: while calculating step 5, the number of digits in the squared number (04) should be equal to number of zeroes in the base(100). Hence in our case, the base 100 has 2 zeros and hence sqaure of 2 is 04 and not just 4.
Now consider another example: Calculate the square of 94. ( following the steps given above...)
1. The neareset power of 10 to given number 94 is 100
2. Hence the base is 100
3. Deficiency = 6
4. Subtract the deficiency from the given number ( 94 - 6 ) = 88
5. Square of deficiency = 36 ( 2 digits)
6. Append the results from step 4 and 5 to get the result. i.e., 8836
Try out calculating squares of 96, 994, 9999995
This sutra means whatever the extent of its surplus, increment it still further to that very extent; and also set up the square of that surplus. This sutra is very useful in calculating the sqaures of numbers nearer(greater) to powers of 10.
Lopana sthapanabhyam means 'by alternate elimination and retention'.
Consider the case of factorization of quadratic equation of type ax2 + by2 + cz2 + dxy + eyz + fzx. This is a homogeneous equation of second degree in three variables x, y, z. The sub-sutra removes the difficulty and makes the factorization simple. The steps are as follows:
i) Eliminate z by putting z = 0 and retain x and y and factorize thus obtained a quadratic in x and y by means of Adyamadyena sutra.
ii) Similarly eliminate y and retain x and z and factorize the quadratic in x and z.
iii) With these two sets of factors, fill in the gaps caused by the elimination process of z and y respectively. This gives actual factors of the expression.
Example 1 : 3x2 + 7xy + 2y2 + 11xz + 7yz + 6z2.
Step (i) : Eliminate z and retain x, y; factorize
3x2 + 7xy + 2y2 = (3x + y) (x + 2y)
Step (ii) : Eliminate y and retain x, z; factorize
3x2 + 11xz + 6z2 = (3x + 2z) (x + 3z)
Step (iii): Fill the gaps, the given expression
= (3x + y + 2z) (x + 2y + 3z)
Example 2 : 3x2 + 6y2 + 2z2 + 11xy + 7yz + 6xz + 19x + 22y + 13z + 20
Step (i) : Eliminate y and z, retain x and independent term
i.e., y = 0, z = 0 in the expression (E).
Then E = 3x2 + 19x + 20 = (x + 5) (3x + 4)
Step (ii) : Eliminate z and x, retain y and independent term
i.e., z = 0, x = 0 in the expression.
Then E = 6y2 + 22y + 20 = (2y + 4) (3y + 5)
Step (iii): Eliminate x and y, retain z and independent term
i.e., x = 0, y = 0 in the expression.
Then E = 2z2 + 13z + 20 = (z + 4) (2z + 5)
Step (iv) : The expression has the factors
(think of independent terms: constants)
= (3x + 2y + z + 4) (x + 3y + 2z + 5).
In connection with factorization of quadratic expressions a sub-Sutra, viz. 'Gunita samuccayah-Samuccaya Gunitah' is useful.
It is intended for the purpose of verifying the correctness of obtained answers in multiplications, divisions and factorizations.
It means in this context: 'The product of the sum of the coefficients(sc) in the factors is equal to the sum of the coefficients(sc) in the product'
Symbolically we represent as sc of the product = product of the sc (in the factors)/p>
Example 1: (x + 3) (x + 2) = x2 + 5x + 6
Now ( x + 3 ) ( x + 2 ) = 4 x 3 = 12 : Thus verified.
Example 2: (x + 5) (x + 7) (x - 2) = x3 + 10x2 + 11x - 70
(1 + 5) (1 + 7) (1 - 2) = 1 + 10 + 11 - 70
i.e., 6 x 8 x -1 = 22 - 70
i.e., -48 = -48 Verified.
1. (2x + 3) (x - 2) = 2x2 - x - 6
2. 12x2 - 23xy + 10y2 = ( 3x - 2y ) ( 4x - 5y )
3. 12x2 + 13x - 4 = ( 3x - 4 ) ( 4x + 1 )
4. ( x + 1 ) ( x + 2 ) ( x + 3 ) = x3 + 6x2 + 11x + 6